Plus je creuse et je me renseigne sur la place du préscolaire dans le portrait des apprentissages en mathématiques et plus je réalise qu’il y a des aptitudes (ou compétences) qui doivent devenir des priorités bien avant le contenu à proprement dit. Pour avoir travaillé le sujet dans d’autres « matières » auparavant, il est devenu clair que ces aptitudes sont génératrices de beaucoup de problèmes d’apprentissage si elles ne sont pas prises en compte et travaillées chez les élèves ayant plus de difficultés.
L’une de ces aptitudes est celle d’apprendre à chercher. Cela inclut de faire découvrir le plaisir de se mettre en mode de recherche, mais aussi d’amener l’enfant à « accepter de devoir chercher même si on ne trouve pas tout de suite »(c’est ce qui la distingue à mes yeux de la curiosité intellectuelle) .
Comme les mathématiques, à l’extérieur de l’école, ne sont que des outils pour résoudre des problèmes quotidiens rencontrés, il faut d’abord se chercher des solutions afin d’utiliser ces outils. Sinon, les outils enseignés demeurent dans la mémoire et disparaissent éventuellement (comme les sinus, cosinus du secondaire, vous vous souvenez?)
Dans ma classe, rechercher m’apparaît sous trois aspects : rechercher toutes les possibilités d’une situation (déduction), rechercher des possibilités dans une infinité de possibilités (créativité) et rechercher différents moyens d’arriver à une solution fermée.
J’offre plusieurs activités pour les trois aspects tout au long de l’année, autant collective qu’individuelle afin de m’assurer que l’enfant se mette en état de recherche.
Pour ce qui est de rechercher dans une infinité de possibilités, les occasions ne se limitent qu’à votre créativité : trouver différents moyens de franchir un obstacle tel un ravin, trouver différentes façons d’emballer un cadeau, trouver différentes versions d’une chanson, etc. On peut l’exploiter autant à la causerie, au petit travail qu’en transition! Et aucune réponse n’est refusée!
Pour ce qui est de rechercher toutes les possibilités d’une situation, cela se résume aux activités ayant recours à la combinatoire. Je vous présente aujourd’hui « Les habits de Léo », activité typique de cette façon de rechercher.
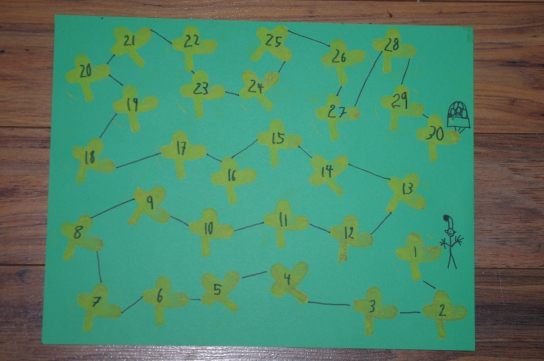
L’activité est simple. Léo doit s’habiller avec un chandail et un short. Il a, dans sa garde-robe, des vêtements de 4 couleurs seulement (jaune, rouge, bleu, vert dans ma classe). Léo veut s’habiller de façon différente chaque jour et son short doit être de couleur différente de son chandail. Les élèves doivent trouver toutes les façons possibles d’habiller Léo.
Je les laisse d’abord manipuler les différentes possibilités avec des carrés de mosaïques qu’ils déposent sur Léo. Puis, lorsqu’ils sont sûrs que toutes leurs possibilités sont différentes, ils peuvent colorier.
Je remets une deuxième feuille à compléter pour les équipes plus rapides à comprendre le principe, car il y a en fait 12 possibilités. On se réunit ensuite pour partager nos trouvailles.
Plus tard, comme atelier individuel, l’enfant aura à compléter la même activité, mais avec seulement 3 couleurs plutôt que 4.
Cette activité est facilement adaptable à différents thèmes. Léo pouvant devenir un pirate, un œuf de Pâques, une voiture, etc.
Et si vous regardez bien, il y a vraiment une tonne de situations de maternelle qui pourraient faire appel à la combinatoire (différentes tours de blocs, différentes productions en art avec seulement 3 ou 4 couleurs, différentes voyelles et consonnes lorsqu’on travaille la conscience phonologique, etc.)
Le troisième aspect de rechercher, visant différents moyens d’arriver à une solution fermée, vaut un article à lui tout seul. Alors, on se reverra!




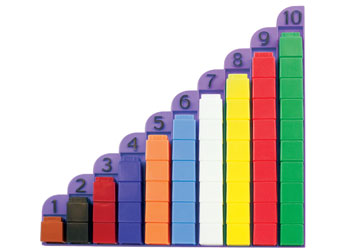
 Il arrive régulièrement que l’enfant compte pour répondre à la question Combien? Mais comprend-il ce qu’il fait?
Il arrive régulièrement que l’enfant compte pour répondre à la question Combien? Mais comprend-il ce qu’il fait?

 Il ne reste que quelques jours avant la fin de l’année scolaire. Ménage, activités spéciales, sorties, ces quelques jours ont très souvent l’apparence d’une fête. Plusieurs activités et rituels prennent place pour aider les élèves à comprendre que la maternelle se termine. L’une d’elles est le compte à rebours.
Il ne reste que quelques jours avant la fin de l’année scolaire. Ménage, activités spéciales, sorties, ces quelques jours ont très souvent l’apparence d’une fête. Plusieurs activités et rituels prennent place pour aider les élèves à comprendre que la maternelle se termine. L’une d’elles est le compte à rebours.